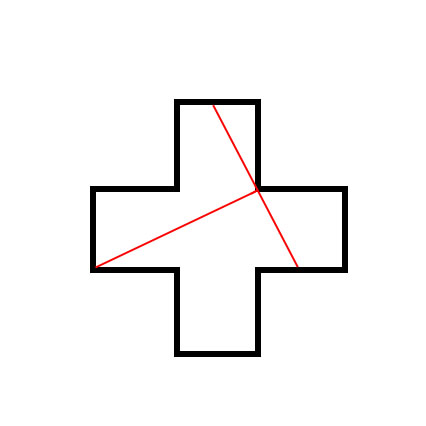
Folgendes (aus 5 kleinen Quadraten zusammengesetzte) Kreuz soll so zerschnitten werden, dass man aus den Teilen ein Quadrat zusammensetzen kann. Alle Teile sollen verwendet werden und keine Lücken oder Überlappungen entstehen und die Schnitte liegen auf nur 2 Geraden (also im Prinzip nicht mehr als 2 Schnitte!)

Eine Erklärung (also Berechnungen zur Lücken- und Überlappungsfreiheit und Nachweis der rechten Winkel und Seitengleichheit) ist hier nicht verlangt.
Bitte aber in der Lösung eindeutig beschreiben, wie die Schnittlinien liegen!
| Lösung |
Die Schnitte erfolgen an den roten Linien, also von einem konvexen Kreuzeckpunkt zum diagonal gegenüberliegenden konkaven Kreuzeckpunkt, durch den senkrecht dazu die zweite Schnittlinie geht. Dass man dann aus den 4 Teilen ein Quadrat zusammensetzen kann, ist auch ohne weiteres Bild nachvollziehbar.
Lösung ausblenden |
|
|









