An einem Siebeneck sind die Zahlen von 1 bis 14 so verteilt, dass an jedem Eck und in jeder Seitenmitte jeweils genau eine Zahl platziert ist.
Allerdings müssen die Zahlen auch so platziert sein, dass die Summe der 3 Zahlen, die entlang einer Seite stehen (also Eckpunktzahl+Seitenmittenzahl+andere Eckpunktzahl), stets die gleiche ist!
Gib eine solche Lösung an (einfach in der Form einer Zahlenkette, die an einem Eckpunkt beginnt, z. B. 1 13 2 7 ...).
Wem diese Herausforderung nicht genug ist, der kann sich ja (ohne Wertung) mal überlegen, ob und ggf. wie das bei jedem beliebigen n-Eck mit ungeradem n funktionieren würde...
| Lösung |
Eine mögliche Lösung ist:
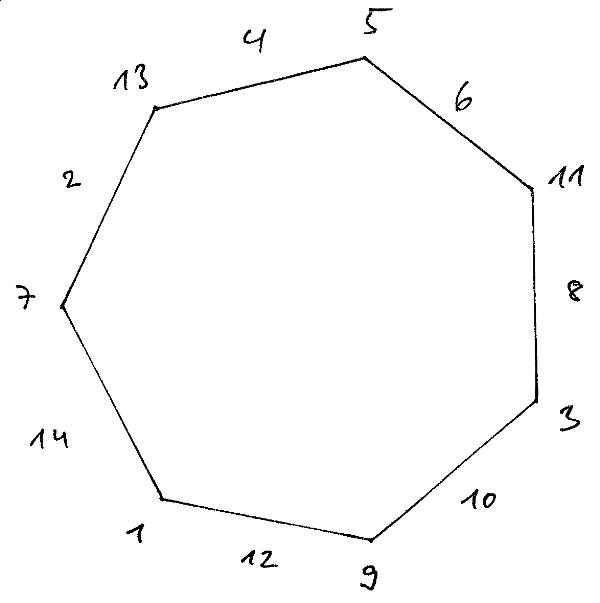
Vielleicht kam dem ein oder anderen die Aufgabenstellung vom Bundeswettbewerb Mathematik her bekannt vor. Daher findet man auch auf dessen Seite die Lösung zur zusätzlichen Herausforderung:
Bundeswettbewerb Mathematik (->Lösungen (2007))
Lösung ausblenden |
|
|









