In der Mitte eines kreisförmigen Sees badet ein hübsches Mädchen mit reichen Eltern. Am Ufer wartet ein Mann mit der Absicht sie zu kidnappen. Nun möchte die Millionärstochter ans rettende Ufer schwimmen ohne dabei direkt mit dem Mann konfrontiert zu werden. Leider kann der Mann viermal so schnell laufen, wie das Mädchen schwimmen kann. Der Entführer bemüht sich natürlich den Abstand zu seinem Opfer stets möglichst klein zu halten. Die Lage des Mädchens scheint aussichtslos...
Wie könnte es das arme Mädchen (nur durch Schwimmen) schaffen, aus dem Wasser zu kommen ohne dem Mann zu begegnen? (Es sei mal angenommen, dass sie ihm an Land entkommen würde...)
| Lösung |
Um die Rechnungen zu vereinfachen, wird zunächst der Kreisradius des Sees auf 1 gesetzt.
Mit der Überlegung, wie weit das Mädchen höchstens zum Ufer zu schwimmen haben darf, wenn der Kidnapper am gegenüberliegenden Seeufer losläuft, kommt man auf Pi/4. Sie müsste also von der Mitte aus rund 21% der Strecke zum Ufer bereits zurückgelegt haben, während der Mann immer noch am gegenüberliegenden Ende ist. Und das geht sogar wirklich: Wenn die Hübsche diese 21% zurücklegt und dann Kreise um den Mittelpunkt schwimmt, hat sie eine etwas höhere Winkelgeschwindigkeit als der Mann. Sie kann also so lange schwimmen, bis sie den Entführer um eine halbe Runde abgehängt hat und dann geradewegs aufs Ufer zusteuern. 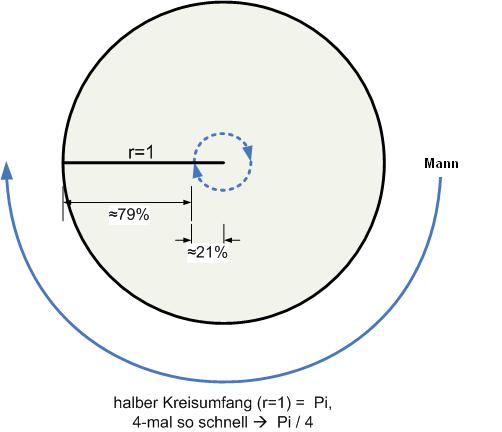
Lösung ausblenden |
|
|







