Ich war neulich zum Geburtstag einer Bekannten meiner Mutter eingeladen – viele Gäste waren da und ich wusste, außer dem Alter der Bekannten (ihr Geburtsjahr war, wie eure wohl auch, im letzten Jahrhundert), nicht viel von ihr. Sie wusste aber, dass ich gerne knifflige Rätsel löse, weshalb sie mir auf meine Nachfrage, wie viele Kinder sie habe, nicht direkt antwortete:
Jeder meiner Söhne hat genau so viele Kinder wie Brüder und jede meiner Töchter genau so viele Kinder wie Schwestern und ich habe so viele Enkelkinder wie ich alt bin.
Aber auch wenn ich davon ausging, dass es keine Halbbrüder oder -schwestern in der Familie gibt, war damit meine Frage nicht beantwortet.
Stimmt, meinte die Bekannte, aber es ist alles klar, wenn ich dir sage, dass ich mehr Töchter als Söhne habe.
Wie alt ist die Bekannte?
| Lösung |
Auch wenn das Rätsel nicht leicht ist, gibt es hier viele Ansätze, die zum Ziel führen, z.B.:
Sei x die Zahl der Söhne und y die der Töchter der Bekannten.
Dann hat sie x(x-1)+y(y-1) Enkelkinder und ist eben so alt.
Nun ist dieser Ausdruck symmetrisch in x und y, d.h. man erhält immer das gleiche Alter, auch wenn man x und y austauscht. Wie kann es also sein, dass in der Angabe, sie habe mehr Töchter als Söhne eine wichtige Information steckt?
Das muss daran liegen, dass es einen Fall gibt, bei dem man bei ein und dem selben Alter auf (mindestens) zwei verschieden Summen x+y kommt (dies war ja Gegenstand meiner Frage im Gespräch: Die Zahl der Kinder – und die Frage war zunächst nicht eindeutig beantwortbar), (mindestens) eine dieser Summen aber von einer gleichen Anzahl von Söhnen und Töchtern ausgeht – die andere Summe muss dann die Anzahl der Kinder angeben.
Also kommen nur noch Alter in Frage, bei denen x=y. Folglich sind das die Ergebnisse von 2x(x-1). Geht man hier die natürlichen Zahlen durch erhält man als Alter:
4, 12, 24, 40, 60, 84, 112…
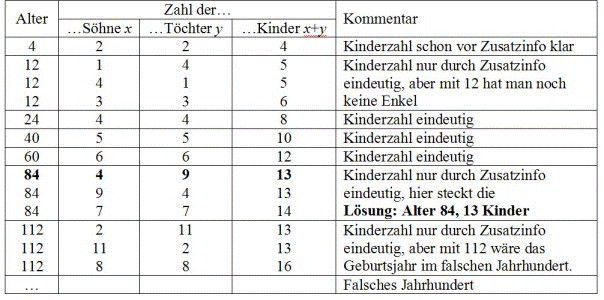
Sucht man sich zu diesen Zahlen noch die möglichen (anderen) Lösungen für x und y stellt man fest:
Lösung ausblenden |
|
|







